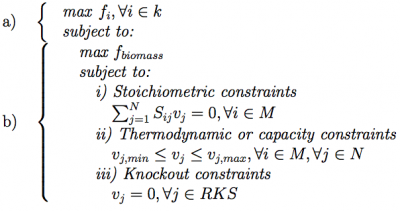Contents
Framework description[edit]
The new version of OptFlux's Strain Optimization plug-in includes all the previous single objective (SO) optimization methods, seamlessly integrated with the new multi-objective (MO) architecture.
In this version of the Optimization plug-in, the following features are available:
- Phenotype methods:
- FBA, pFBA, ROOM, MOMA, Linear MOMA, MiMBL
- Optimization methods:
- EA, SA, SPEA2
- Single and multi-objective
- Types of Knockout:
- Reactions, Genes
- Over/under expression optimization
The Archive Manager[edit]
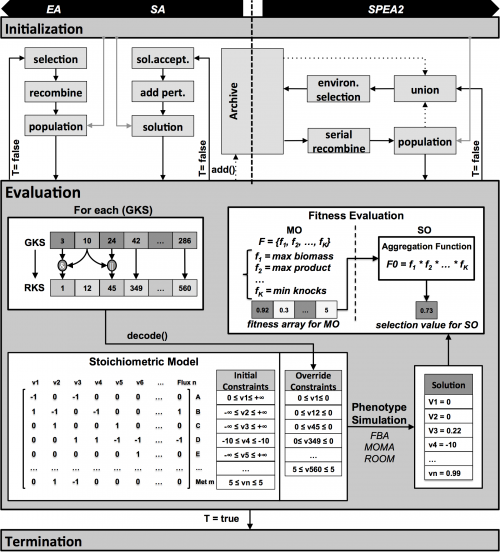
In this version of OptFlux, some changes were applied to the EA and SA algorithms, regarding the information that is kept during each run, although not changing their functioning nor the best final solution. The major change was the implementation of an archive that keeps the best solutions found by the EA and SA during the run. This is not used by the algorithms for selection or for creating new solutions, but allows having a richer final result. The archive runs in a parallel thread, and smartly manages the solutions that are kept, removing duplicate solutions and non-better super solutions of already existing ones.
Solution Simplification[edit]
The end step of an optimization procedure is the solution simplification. These heuristics, although intelligent, may generate solutions that include unnecessary knockouts/regulations. To prevent this, all the non-meaningful genetic modifications are removed from the solutions.
Representation scheme and operators[edit]
The optimization problem here addressed consists in selecting, from a set of genes of an organism (represented in the respective metabolic model), a subset to be deleted (or over/under regulated), in order to optimize a set of objective functions. The encoding of a solution is achieved by a set-based representation (Rocha et al., 2008), where only gene deletions are represented. The representation scheme uses variable-sized genomes and hence sets with distinct cardinalities can compete within the search process. Two types of reproduction operators were used: crossover and mutation.
Solution decoding and evaluation[edit]
Each solution is represented as a gene knockout set GKSi,t (i-th solution of the population at generation t) containing a list of indexes for genes in the model, a subset of the full set of genes that can be deleted (e.g. essential genes are no allowed). Transcriptional/ translational information is encoded in the model as a set of Gene Reaction (GR) associations, represented by Boolean rules, including AND and OR operations.
Each GKS is converted through those rules into a reaction knockout set (RKSi,t). Each RKS consists of a set of integer values between 1 and N, where N is the number of reactions in the model. When simulating this solution, for each reaction in this set, the flux is forced to be 0, therefore disabling it from the model. The process proceeds with the phenotype simulation of the mutant using one of the available methods. In the experiments performed within this work, the FBA method was used, but any of the methods available within the OptFlux framework can be used (e.g. MOMA or ROOM). FBA is a constraint-based approach where feasible flux distributions are mainly defined by three types of constraints (Equation 1b): i) stoichiometric constraints, defining the mass balance equations over internal metabolites assuming steady-state (in the formulation vj corresponds to the flux of re- action j and Sij, stands for the stoichiometric coefficient of metabolite i in reaction j); ii) thermodynamic or capacity constraints, mainly defining re- action reversibility (vj,min for the lower limit and vj,max for the upper limit of the reaction vj); and iii) those imposed by the knockouts defined in the respective RKS. FBA uses linear programming to determine the optimal flux distributions using a specified objective function, maximizing a flux representing biomass production.
The optimization problem can be formulated as:
where N corresponds to the set of reactions and M to the set of metabolites in the model.
The layer (a) addresses the objective functions at the bioengineering level to be addressed by the MO algorithm, while the layer (b) depicts the constraints of the inner phenotype simulation (cellular level). In this bi-level formulation the strain optimization and the phenotype simulation methods can be chosen independently from all available options (e.g. SPEA2, EA or SA in a) and FBA, MOMA or ROOM in b)). The output of phenotype simulation is the set of flux values for all reactions in the model. These are used by the optimization algorithms to compute the fitness value of the solution, using an appropriate objective function.
Performing strain optimization in OptFlux[edit]
The operation can be accessed in the menu Optimization->Evolutionary...
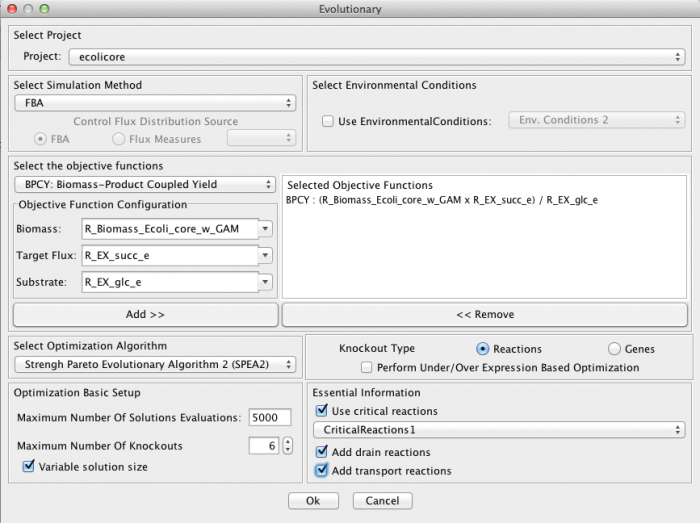
Optimization dialog and preferences[edit]
- Select Simulation method - The method used to perform the phenotype simulation layer.
- FBA, pFBA, MOMA, LinearMOMA, ROOM and MIMBL are available.
- Select Environmental Conditions - The list of available environmental conditions available for this project.
- Select the objective functions
- OptFlux support multiple-criteria optimisation, this means that you can select several objective functions to optimize at the same time.
- BPCY: Biomass-product coupled yield
- YIELD: Product Yield with minimum biomass
- Max/Min of reaction flux value
- Max/Min of the number of knockouts
- Max/Min of the sum of flux measures
- You must configure each objective function individually and then press the Add>> button to add it to the list (on the right).
- OptFlux support multiple-criteria optimisation, this means that you can select several objective functions to optimize at the same time.
- Select Optimization Algorithm - The optimization method to use
- Evolutionary Algorithm (EA)
- Simulated Annealing (SA)
- Strength Pareto Evolutionary Algorithm 2 (SPEA2) - This method is natively multi-objective, thus prone to provide better solutions when multiple objective functions are used.
- Knockout Type
- Reactions or Genes
- Perform Under/Over expression based optimization. This option allows to compute regulations for the activity of reactions/expression of genes instead of simple deletion.
- Optimization Basic Setup
- Maximum Number of Solution Evaluations - The number of simulations allowed for this optimization. The larger the number, the better the chances of finding optimal solutions, but the longer it will take.
- Maximum Number of Knockouts - The maximum number of deletions/regulations allowed.
- Variable size solution. When selected, the size of the solutions is not fixed and can vary up to the maximum previously configured.
- Essential Information - Depending on whether this is a Reaction of Gene optimization, you can select a set of reactions/genes that must never be considered for deletion. This set can be computed automatically by OptFlux (see Determine Critical Genes/Reactions)
Execution and options[edit]
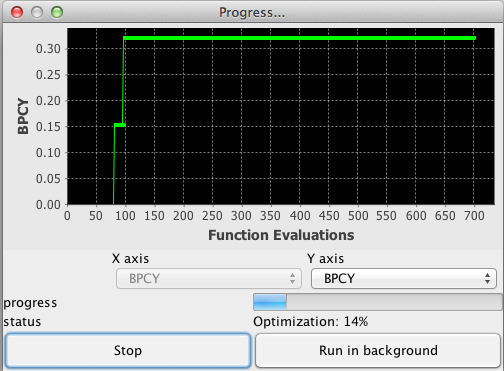
When performing optimizations, one of the following dialogs will be displayed, depending on whether you select only one objective function (Left) or several (Right)
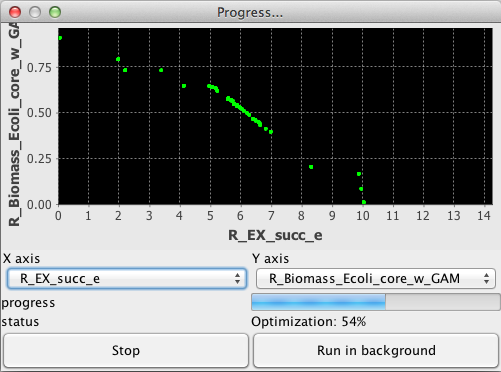
In the case of single-objective optimization, the chart displays the best solution found relative to the number of evaluation functions performed. In the event of multi-objective optimization, the chart displays the current state of the pareto-front, that is the trade-off between the selected objectives for solutions kept in the archive.
In both cases you can stop the optimization process at any time, and this will call the solution simplification process immediately.
Analysing optimization solutions[edit]
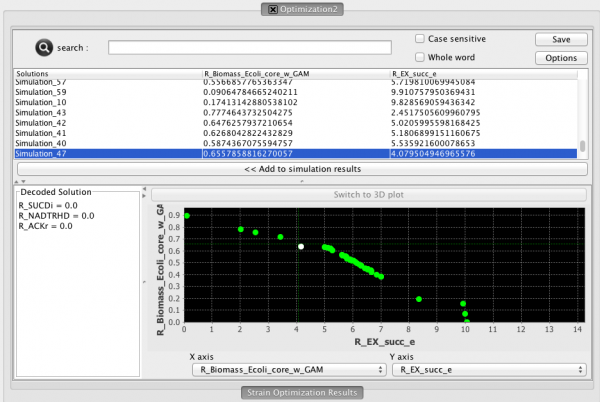
When the optimization procedure completes, the solutions will be sent to the OptFlux clipboard:
Clicking it will launch the view on the right:
- The optimization view contains three distinct sections:
- (TOP) The List of solutions and respective fitnesses
- (BOTTOM-LEFT) The decoded solution (you must select a solution either in the list or in the chart). This list will display the suggested gene/reaction) deletions or over/under regulations for the selected solution
- (BOTOM-RIGHT) The chart displaying the trade-of solutions (This chart is displayed as a pareto front when multiple objective functions were used, otherwise, the solutions will be ploted with the single objective function as the Y axis only)
- You can zoom-in or out of the chart using the mouse.
- You can click any point and the corresponding solution will be highlighted in the top list.
- Pressing the << Add to simulation results button, will send the selected solutions to the list of simulations in the clipboard
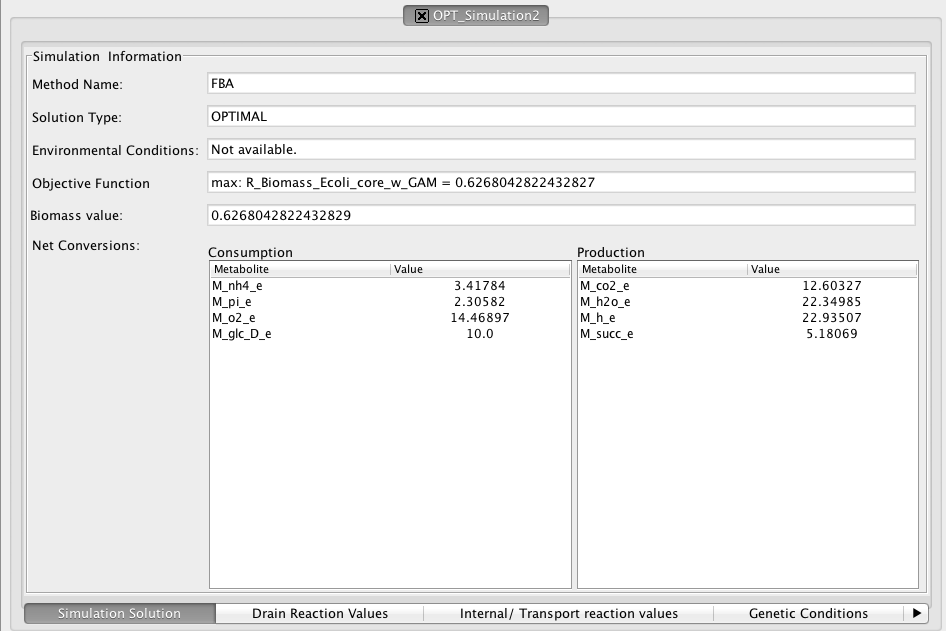
Aftewards, each simulation can be individually analysed with full detail using the simulation view.